Research Interests
Cosmology
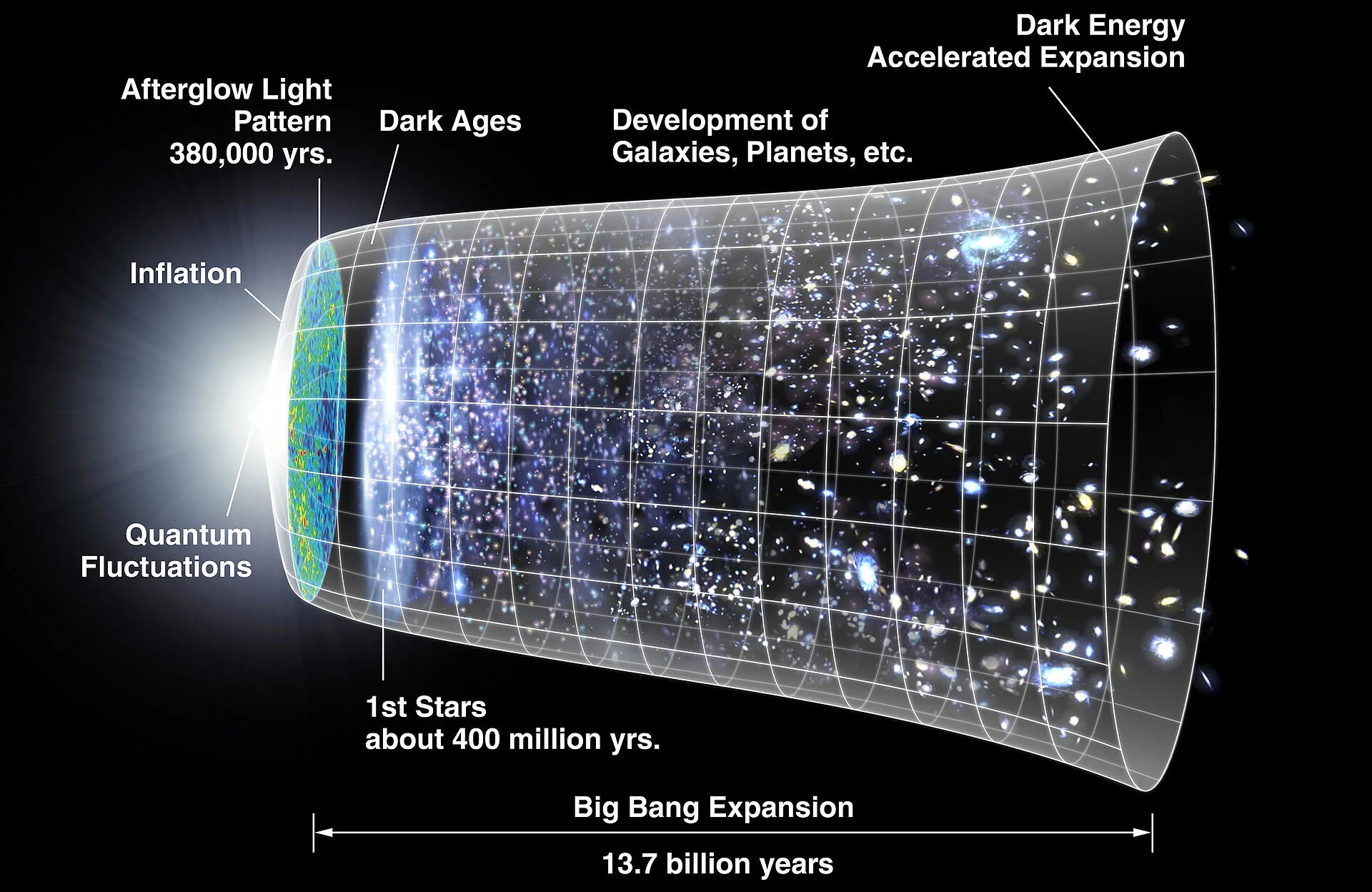
We are in a golden time for precision cosmology. There are so many open questions; previous assumptions are being questioned (could space be positively curved?), and we have the Hubble constant tension between local measurements and analysis of the cosmic microwave background (CMB) which probes the early universe - this may be pointing to new physics. In the next decade a host of exciting new observatories, both space- and ground-based, will be launched and become operational (James Web Space Telescope, Euclid satellite, Large Synoptic Survey Telescope, and the Thirty Meter Telescope are some examples), and they will deliver a deluge of precision cosmological data, from which we will be able to learn so much more about dark matter, dark energy and inflation.
Perturbation Theory, Asymptotic Methods
A large majority of the mathematical models that are relevant to problems in both the natural sciences and humanities are intractable; not exactly solvable, in the sense that we cannot write down a closed form solution. Mathe often similar to exactly solvable problems in a variety of ways. Methods of perturbation theory are some of the best tools we have to solve these problems, by relating their solution to that of a similar problem that is exactly solvable. This approach has been highly successful in theoretical physics, including the breakthrough of Feynman, Schwinger and Tomanaga in Quantum Electrodynamics. In recent years much progress has been made in the area of resurgence theory. Typical perturbation methods express the solution of an equation as an asymptotic power series, with terms proportional to polynomial powers of a perturbation parameter. Resurgence theory uses transseries that contain terms with the regular polynomial factors, factors exponentially smaller than all terms in (standard) perturbation theory, and logarithmic terms as well. These are natural objects because they have very strong closure properties, so that various operations on quantities represented as transseries do not give rise to problematic terms. In quantum mechanics and quantum field theory, terms grouped by the exponential factors represent instantons of the theory. In general, resurgence theory establishes a strong link between perturbative and non-perturbative regimes.